Locomotion is the means by which systems use internal shape changes to move through the world, and is one of the most fundamental actions performed by robots and living organisms.
Geometric mechanics is the application of differential geometry to problems in classical mechanics. By studying locomotion with geometric tools, we can make rigorous statements about systems’ motion capabilities.
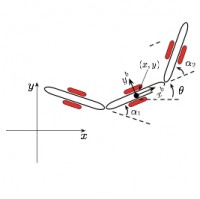
The three-link kinematic snake shown above propels itself by using shape changes (changes to the internal joint angles) to push against the passive wheels on the links. These wheels act as nonholonomic constraints that prevent lateral translation while allowing free longitudinal and rotational motion of each link. Using the framework of geometric mechanics, this locomotory effect can be quantified and qualified, leading to the identification of patterns of motion that produce a desired net displacement.
Geometric locomotion studies have produced powerful tools for system analysis. Unfortunately, the inherent basis of these studies in differential geometry often acts as a barrier to entry for non-specialists who otherwise might benefit from applying the resulting tools to a broader set of systems. In many cases, however, the largest barrier is one of language rather than concept, in that the differential geometric terms in which the results are presented have dual concepts in vector calculus.
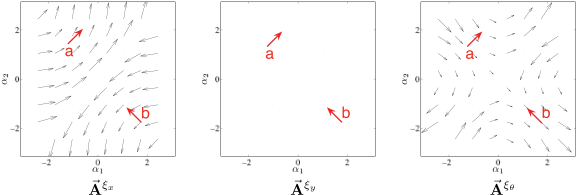
One of the philosophies of our work is to use more familiar vector-calculus terms wherever possible, noting the more formal nomenclature but keeping it out of the main development if a simpler description will suffice. Some of these simplified developments also lead to novel graphical representations of system kinematics. For instance, a one-form is a structure commonly encountered in differential geometry, defined as a “linear map from vectors to scalars.” This structure is functionally equivalent to the more familiar concept of a vector field with a dot product, and thinking in such vector terms provides an avenue for a newcomer to the field to draw on prior knowledge and intuition. Making this vector analogy led us to develop the connection vector field as an illustration of the local connection, a set of one-forms used in geometric mechanics to describe the relationship between shape velocities and the position velocities they induce.